12th Chemistry guide Exam Questions of Chapter 1

Chapter 1 – Solid state

12th chemistry guide

12th chemistry guide Standard Important question based on CBSE board curriculum and corresponding to the recent 12th chemistry syllabus in text questions.
By rehearsing these 12th chemistry significant inquiries, understudies will actually want to rapidly survey every one of the thoughts shrouded in the part and plan for the Class 12 Yearly assessments as well as other selection tests like NEET and JEE.

Why are solids rigid?(Chemistry book)

Solids are rigid primarily due to the strong forces of attraction between their constituent particles. The particles in a solid are typically closely packed and held in fixed positions relative to each other.
The primary factors contributing to the rigidity of solids are: (i)Strong Intermolecular forces, (ii)Lattice Structure, (iii)Short Range Order and (iv)Low Kinetic Energy
Type

Why do solids have a definite volume?(Chemistry book)

Solids have a definite volume because their particles are closely packed and held in fixed positions relative to each other. This characteristic is a result of the strong forces of attraction between the particles in a solid.

Classify the following as amorphous or crystalline solids: (Chemistry book)

Polyurethane,
naphthalene, benzoic acid, teflon, potassium nitrate, cellophane, polyvinyl
chloride, fibre glass, copper.

• Polyurethane: Amorphous
• Naphthalene: Crystalline
• Benzoic Acid: Crystalline
• Teflon: Amorphous
• Potassium Nitrate: Crystalline
• Cellophane: Amorphous
• Polyvinyl Chloride (PVC): Amorphous (soft PVC) or Crystalline (rigid PVC)
• Fiberglass: Amorphous
• Copper: Crystalline

Why is glass considered a super cooled liquid?(Chemistry book)

Glass is basically an amorphous solid. It does not form a crystalline structure. So, the constituent particles of the glass can move.

The reason for this uneven thickness in historical glass windows is not due to the glass flowing as a liquid. Instead, it is a result of the manufacturing process. In the past, glass panes were often made by pouring molten glass onto a flat surface and then spinning or blowing it into a disc shape. The center of the disc would be thicker than the edges. The uneven thickness is a consequence of the production methods, not the glass flowing over time.

In summary, glass is not a supercooled liquid; it is an amorphous solid. The notion that glass is a supercooled liquid is a myth, and the uneven thickness in historical glass windows is a result of the manufacturing process, not the slow flow of the glass over time.

Refractive index of a solid is observed to have the same value along all directions.
Comment on the nature of this solid. Would it show cleavage property?(Chemistry book)

As isotropic solid has the same value of physical properties when measured along different directions.The nature of a solid being isotropic in terms of refractive index typically implies a lack of preferential alignment or orientation of its constituent particles or structural elements. This is in contrast to an anisotropic material, where the refractive index may vary with direction due to variations in the arrangement of particles.

In summary, if the refractive index of a solid is the same along all directions, it suggests isotropy in optical properties, and the material is less likely to show cleavage property in the context of a crystalline structure. Isotropic materials are often associated with amorphous solids or those with a disordered atomic arrangement.

Classify the following solids in different categories based on the nature of
intermolecular forces operating in them:(Chemistry book)

Potassium sulphate, tin, benzene, urea, ammonia, water, zinc sulphide,
graphite, rubidium, argon, silicon carbide

• Potassium sulphate: Ionic (due to the presence of K⁺ and SO₄²⁻ ions)
• Tin: Metallic (metallic bonding)
• Benzene: Molecular (dispersion forces, and some resonance stabilization)
• Urea: Molecular (hydrogen bonding)
• Ammonia: Molecular (hydrogen bonding)
• Water: Molecular (hydrogen bonding)
• Zinc sulphide: Ionic (due to the presence of Zn²⁺ and S²⁻ ions)
• Graphite: Covalent (with delocalized electrons, forming layers)
• Rubidium: Metallic (metallic bonding)
• Argon: Atomic (dispersion forces)
• Silicon carbide: Covalent (very strong covalent bonds between Si and C)

Here’s a breakdown:

• Ionic solids: Potassium sulphate, Zinc sulphide.
• Metallic solids: Tin, Rubidium.
• Molecular solids: Benzene, Urea, Ammonia, Water.
• Covalent network solids: Graphite, Silicon carbide.
• Atomic solid: Argon.

Solid A is a very hard electrical insulator in solid as well as in molten state and melts at extremely high temperature. What type of solid is it?(Chemistry book)

The given properties are the properties of a covalent or network solid. Therefore, the given solid is a covalent or network solid. Examples of such solids include diamond(C) and silicon carbide(SiC).

So, Solid A is likely a covalent network solid due to its hardness, electrical insulating properties, and high melting point.

Ionic solids conduct electricity in molten state but not in solid state. Explain Question. (Chemistry book)

In ionic compounds, electricity is conducted by ions. In solid state, ions are held together by strong electrostatic forces and are not free to move about within the solid. Hence, in molten state or in solution form, the ions are free to move and can conduct electricity.

In the solid state:

• Fixed Positions: In an ionic solid at room temperature, the constituent ions are held in fixed positions in the crystal lattice. The electrostatic forces of attraction between oppositely charged ions are strong, preventing the ions from moving freely. As a result, the solid does not conduct electricity because there are no mobile charge carriers (ions) available to carry an electric current.

In the molten state:

• Breaking of Bonds: When an ionic solid is heated to a sufficiently high temperature, it undergoes melting, and the strong ionic bonds holding the ions in fixed positions are broken.
• Mobile Ions: In the molten state, the ions become mobile because they are no longer confined to fixed positions. The high temperature imparts enough energy to the ions to overcome the electrostatic forces, allowing them to move freely.
• Conduction of Electricity: Because of the presence of mobile ions, the molten ionic compound becomes capable of conducting electricity. The ions can now migrate and carry an electric current through the molten material.

In conclusion, ion mobility affects an ionic solid’s capacity to conduct electricity. Non-conductivity results from the ions’ fixed positions and inability to move in the solid state. Ionic bonds are broken in the molten state, making ions mobile and promoting the conduction of electricity.

What type of solids are electrical conductors, malleable and ductile?(Chemistry book)

Metallic solids are electrical conductors, malleable, and ductile.

Give the significance of a ‘lattice point’.(Chemistry book)

The significance of a lattice point is that each lattice point represents one constituent particle of a solid which may be an atom, a molecule (group of atom), or an ion.

Name the parameters that characterise a unit cell.(Chemistry book)

The unit cell is the smallest repeating unit in a crystal lattice, and its characteristics are described by several parameters. The key parameters that characterize a unit cell are: Edge Lengths (a, b, c), Angles Between Edges (a,b,c,α,β,γ), Axial Lengths and Angles, Volume (V) and etc..

Distinguish between(Chemistry book)

(i) Hexagonal and monoclinic unit cells

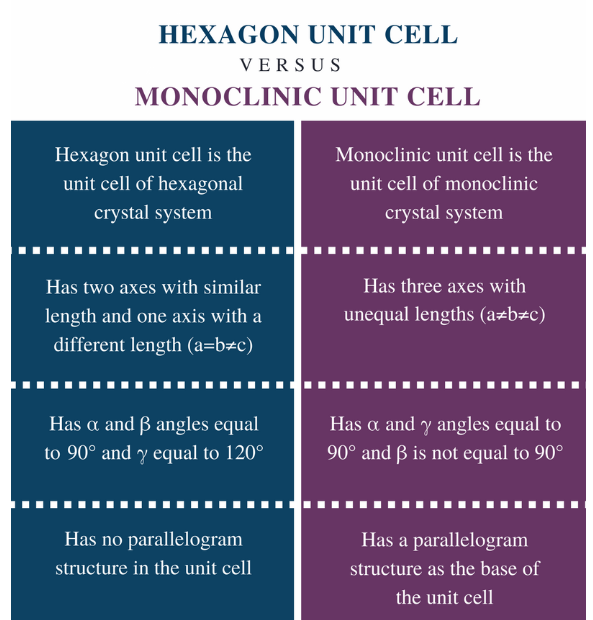
(ii) Face-centred and end-centred unit cells

Explain how much portion of an atom located at (i) corner and (ii) bodycentre of a cubic unit cell is part of its neighbouring unit cell.(Chemistry book)

In a cubic unit cell, atoms are located at various positions, such as corners and the body center. The fraction of an atom that belongs to its neighboring unit cell depends on the specific type of unit cell. Let’s consider the two cases:

(i) Fraction of Atom at Corner of a Cubic Unit Cell:

In a simple cubic unit cell, there is one atom at each corner. Since each corner atom is shared by eight adjacent unit cells, the fraction of the atom that belongs to the neighboring unit cell is 1/81/8. This is because each corner atom is shared equally by eight adjacent cubes, and thus, 1/81/8 of the atom is in the neighboring unit cell.

(ii) Fraction of Atom at Body Center of a Cubic Unit Cell:

In a body-centered cubic (BCC) unit cell, there is one atom at the center of the cube. This atom is not shared with any other unit cell, and it is entirely contained within the unit cell. Therefore, the fraction of the atom at the body center that belongs to the neighboring unit cell is 00.

A compound is formed by two elements M and N. The element N forms ccp and atoms of M occupy 1/3rd of tetrahedral voids. What is the formula of the compound?(Chemistry book)

In a close-packed structure, such as face-centered cubic (FCC) or cubic close packing (CCP), each sphere (or atom) is in contact with 12 others. In a CCP arrangement, the coordination number is 12.

When atoms of element M occupy 1/3rd of the tetrahedral voids, it implies that every fourth tetrahedral void is occupied by an atom of M. The coordination number of tetrahedral voids is 4.

Now, let’s consider the ratio of atoms of M to atoms of N in the structure.

For every atom of M, it occupies 1/3 of a tetrahedral void, and there are 4 tetrahedral voids per atom.

Ratio of atoms of M to atoms of N=13×number of atoms of Mnumber of atoms of NRatio of atoms of M to atoms of N=number of atoms of N31​×number of atoms of M​

Now, the total number of tetrahedral voids is equal to twice the number of atoms in the CCP lattice (since each atom in the CCP lattice contributes to two tetrahedral voids).

So, the ratio becomes:

13×12×number of atoms in CCPnumber of atoms of Nnumber of atoms of N31​×21​×number of atoms in CCP​

Since each atom in the CCP lattice has a coordination number of 12, the number of atoms in CCP is 12.

13×12×12number of atoms of Nnumber of atoms of N31​×21​×12​

2332​

So, the ratio of atoms of M to atoms of N is 2332​. Therefore, the empirical formula of the compound is M2​N3​.

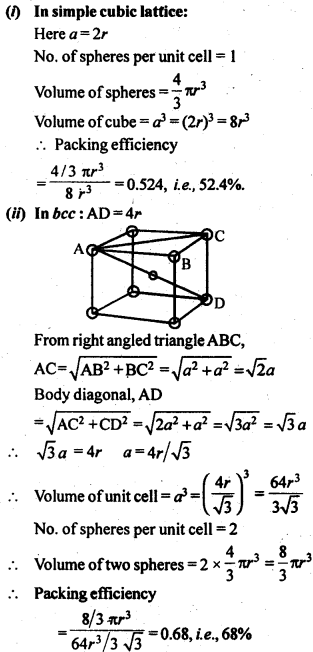
Which of the following lattices has the highest packing efficiency (i) simple
cubic (ii) body-centred cubic and (iii) hexagonal close-packed lattice?(Chemistry book)

The packing efficiency of a crystal lattice is the fraction of space filled by the constituent particles (atoms, ions, or molecules). It is influenced by the arrangement of particles within the unit cell. Let’s compare the packing efficiencies of the given lattices:

(i) Simple Cubic (SC) Lattice:

• Each particle in the simple cubic lattice is at the corners of the cube.
• The packing efficiency for a simple cubic lattice is approximately 52.4%.

(ii) Body-Centered Cubic (BCC) Lattice:

• Each particle in the body-centered cubic lattice is at the corners and at the center of the cube.
• The packing efficiency for a body-centered cubic lattice is approximately 68%.

(iii) Hexagonal Close-Packed (HCP) Lattice:

• In a hexagonal close-packed lattice, the particles are arranged in a way that maximizes packing efficiency.
• The packing efficiency for a hexagonal close-packed lattice is approximately 74%.

An element with molar mass 2.7×10-2 kg mol-1 forms a cubic unit cell with edge length 405 pm. If its density is 2.7×103 kg m-3, what is the nature of the cubic unit cell?(Chemistry book)

What type of defect can arise when a solid is heated? Which physical property is affected by it and in what way?(Chemistry book)

When a solid is heated, it can undergo a type of defect known as a “thermal or vacancy defect” or “Schottky defect.” This type of defect commonly occurs in ionic solids.

Thermal (Vacancy) Defect (Schottky Defect):

• Cause: It arises due to the creation of vacancies (missing ions) in the crystal lattice when the solid is heated.
• Temperature Effect: Higher temperatures provide energy to the lattice ions, allowing some of them to move out of their positions, creating vacant sites.
• Affected Materials: Common in ionic compounds, especially those with a high coordination number.

Physical Property Affected:

• Density: The presence of vacancies decreases the effective number of ions in the crystal lattice, leading to a decrease in density.

Effect on Physical Property:

• Decrease in Density: The introduction of vacancies reduces the mass of the crystal without significantly changing its volume. As a result, the overall density decreases.

This defect is often observed in solids with a high concentration of vacancies. While it can occur during heating, it’s important to note that not all solids exhibit this type of defect, and its occurrence depends on factors such as the type of solid, temperature, and pressure.

What type of stoichiometric defect is shown by(Chemistry book):

(i) ZnS (Zinc Sulfide):

• Type of Defect: Frenkel Defect
• Explanation: In a Frenkel defect, one of the ions (usually a smaller cation) is displaced from its normal lattice site to an interstitial site (a vacant space between lattice points). In the case of ZnS, zinc ions (Zn²⁺) may move to interstitial sites within the crystal lattice.

(ii) AgBr (Silver Bromide):

• Type of Defect: Schottky Defect
• Explanation: In a Schottky defect, equal numbers of cations and anions are missing from their lattice sites, creating vacancies in the crystal. In AgBr, silver ions (Ag⁺) and bromide ions (Br⁻) may be missing from their regular positions, leading to a Schottky defect.

Explain how vacancies are introduced in an ionic solid when a cation of higher valence is added as an impurity in it(Chemistry book)

When a cation of higher valence is added as an impurity in an ionic solid, vacancies are introduced in the crystal lattice due to charge imbalance. This process can be explained with an example:

Let’s consider an ionic solid represented by the formula MX, where M is a metal cation of lower valence and X is an anion. The compound has a specific stoichiometry, and the crystal lattice is in an ideal arrangement.

Now, suppose a cation of higher valence, represented by M’, is added as an impurity. The higher valence implies that M’ has more positive charges than M. The addition of M’ creates a charge imbalance in the crystal lattice because the total positive charge has increased.

To maintain charge neutrality, some cations (M+) need to be replaced by the cations of higher valence (M’+) in the crystal lattice. However, since M’ has more positive charges, not all of them can replace M+ without creating an excess of positive charge. As a result, some vacancies are introduced to compensate for the excess positive charge.

The process can be summarized as follows:

• Cation Replacement: Cations of higher valence (M’+) replace some of the cations of lower valence (M+).
• Charge Imbalance: The replacement leads to an excess positive charge in the crystal lattice due to the higher valence of M’.
• Vacancies Formation: To maintain charge neutrality, vacancies (unoccupied spaces) are introduced in the lattice. These vacancies correspond to the missing cations of lower valence (M+) that were replaced by the higher-valence cations (M’+).

This phenomenon is an example of a Schottky-type stoichiometric defect, where equal numbers of cations and anions are missing from their lattice positions, resulting in the formation of vacancies. The vacancies serve to balance the excess positive charge introduced by the higher-valence cations.

Ionic solids, which have anionic vacancies due to metal excess defect, develop colour. Explain with the help of a suitable example.(Chemistry book)

The development of color in ionic solids due to metal excess defects, particularly anionic vacancies, is often associated with the presence of transition metal ions. This phenomenon is known as color centers, and it occurs when certain metal ions are present in the crystal lattice in a state other than their usual oxidation state. The color arises due to the absorption of light by these color centers.

Let’s take an example to illustrate this:

Example: F-centers in NaCl (Sodium Chloride):

In sodium chloride (NaCl), if some sodium ions are replaced by excess silver ions (Ag⁺) in the crystal lattice, it can lead to the formation of F-centers (color centers). The excess Ag⁺ ions do not contribute to the normal ionic bonding but instead create vacancies in the anionic sub-lattice.

The process can be represented as follows:

Here, x represents the concentration of excess Ag⁺ ions.

The vacancies created in the chloride sub-lattice are known as anionic vacancies. These vacancies create an electron deficiency in the crystal lattice, and the electrons associated with these vacancies absorb visible light, leading to the development of color. The absorbed light corresponds to specific wavelengths, and the color observed is complementary to the absorbed light.

In the case of silver in NaCl, the development of a yellow color is often observed due to the presence of F-centers. The yellow color is a result of the absorption of blue light by the F-centers.

In summary, the introduction of metal excess defects, particularly anionic vacancies, in ionic solids with transition metal ions can lead to the development of color centers, giving the material a distinctive color.

A group 14 element is to be converted into n-type semiconductor by doping it with a suitable impurity. To which group should this impurity belong?(Chemistry book)

An n-type semiconductor conducts because of the presence of extra electrons. Therefore, a group 14 element can be converted to n-type semiconductor by doping it with a group 15 element.

What type of substances would make better permanent magnets, ferromagnetic or ferrimagnetic. Justify your answer.(Chemistry book)

Ferromagnetic substances would make better permanent magnets because when the ferromagnetic substance is placed in a magnetic field, all domains get oriented in the direction of magnetic field and strong a magnetic effect is produced.

Check our dark humor or memes here.